행렬식(determinant) 알아보기 + 구현

책을 읽다가 행렬식(determinant)에 대한 노트를 읽었는데, 기하학적으로 설명된 부분에 궁금한 점이 생겨서 정리해보고자 한다.

2X2 행렬

책에서는 2X2 행렬에 대해서 \(det(A)~=~a_{11}a_{22} - a_{12}a_{21}\) 을 이렇게 설명하고 있었다.

행렬 \(A~=~\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\) 의 행렬식은 두 개의 열 벡터 \(\begin{pmatrix} a_{11} \\ a_{21} \end{pmatrix}\) 와  \(\begin{pmatrix} a_{12} \\ a_{22} \end{pmatrix}\) 를 두 변으로 하는 평행사변형의 면적이다.

그럼 행렬 \(\begin{pmatrix} 3 & 2 \\ 1 & 4 \end{pmatrix}\) 를 2차원 좌표평면에 아래처럼 그릴 수 있고, 행렬식은 이 사각형에 대한 넓이를 계산한다는 의미라는 것이다.

[[3, 2], [1, 4]] 를 2차원 평면 위에 표시

궁금한 점은 2가지인데, 하나는 \(det(A)~=~a_{11}a_{22} - a_{12}a_{21}\) 로 구한 값 (1)과 평행사변형의 넓이 (2), 그리고 벡터의 내적으로 구해지는 넓이 (3)가 모두 같은 값인가? 가 첫 번째 의문점이었다.

감사하게도 먼저 깔끔하고 자세하게 정리를 해주신 분의 글이 있었다.
두 번째 궁금증 역시 아래의 포스트를 참고해서 해결할 수 있었다.

[Linear Algebra] Lecture 20-(2) 행렬식(Determinant)의 기하학적 해석(Geometrical Analysis)

위 포스트에 따르면 결과적으로 (1), (2), (3)은 모두 같은 값으로 계산된다. 즉, 2X2 행렬의 행렬식은 그 넓이를 계산하는 것이 맞다는 것이다.

 

3x3 행렬

두 번째 궁금증은, 그럼 3X3 행렬은 3차원 점들에 대해서 부피를 구한다는 의미인가? 이다.

먼저 이것을 기하학적으로 이해하기 위해서, 2X2 행렬 \(\begin{pmatrix} 3 & 2 \\ 1 & 4 \end{pmatrix}\) 에 한 층 쌓아서 \(\begin{pmatrix} 3 & 2 & 0 \\ 1 & 4 & 0 \\ 2 & 1 & 2 \end{pmatrix}\) 를 만들어보자. 기존의 2개의 점은 z=0 인 평면에 둔다.

위에서처럼 이것들을 행 벡터로 생각하면 세 점 (3, 2, 0), (1, 4, 0), (2, 1, 2) 으로 그려볼 수 있을 것이라 생각했다.
(3X3의 정방행렬이고, 행렬식의 결과값은 하나의 상수이므로 뒤집어도 계산 과정에는 문제가 없다.)

3차원으로 옮기고 점을 하나 추가해본다.

그럼 기존에 2X2 행렬은 노란색 부분처럼 표시된다는 것이고, 새로 추가된 점 (2, 1, 2) 에 대해서도 평행하게 모서리를 전부 그려보면 하나의 직육면체가 나온다.

3x3 행렬이 나타내는 기하학적인 형태

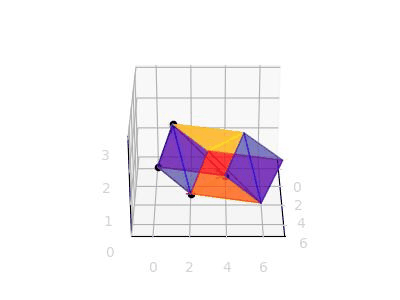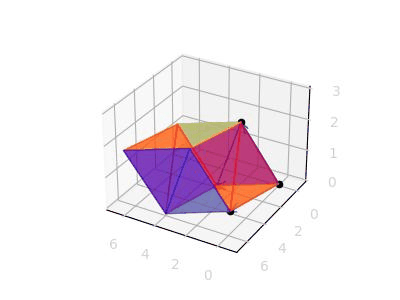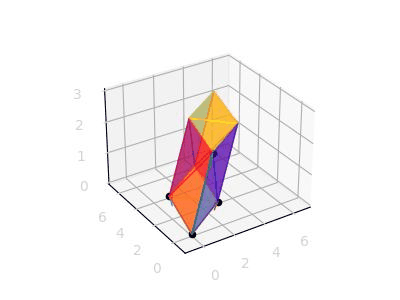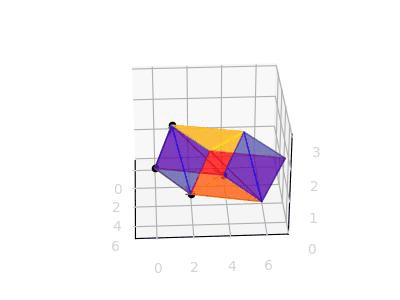
이제 det(A)는 위와 같은 직육면체에 대한 부피를 구하게 된다는 것이다.
(각 평면이 깜빡거리는 이유는 matplotlib 에서 z-order 관련한 버그(?)이다. 해결하려면 다른 라이브러리인 Mayavi 를 쓰면 된다고 하지만 지금은 굳이...)

3X3 행렬에 대해서도 첫 번째 의문이었던 (1), (2), (3) 모두 위 포스트에서 정리가 되어있다. 새로 추가한 점에 대한 벡터가, 노란색 평면에 수직이 아니라서, 계산 과정이 복잡해지지만 결국은 부피가 잘 구해진다.

---

NXN 행렬

그럼 4X4, 5X5 행렬에 대해서도 가능하다는 것인데, 크기별로 행렬식에 대한 공식이 정확히 어떻게 되는 것이고 어떻게 구할 수 있는가?

NumPy 함수

먼저, 다행스럽게도 NumPy에서 함수를 제공한다.

from numpy.linalg import det

det([[3,2,0],[1,4,0],[2,1,2]])
# 20.0

레퍼런스는 아래를 참고하면 된다.

numpy.linalg.det — NumPy v1.24 Manual

직접 구현해보기

행렬 \(A~=~\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}\) 의 행렬식은 2X2 행렬식으로부터 아래와 같이 정의할 수 있다.

여기서 재귀적으로 4X4 이상의 행렬도 정의할 수 있는데, 아래처럼 색칠해보면 규칙을 확인하기 쉽다.

이것을 파이썬 함수로 직접 작성해보면 아래와 같다.

def submatrix(a: list, col_i: int) -> list:
    m = []
    n = len(a)
    for i in range(1, n):
        row = []
        for j in range(n):
            if col_i == j: continue
            row.append(a[i][j])
        m.append(row)
    return m


def det(a: List[list]) -> float:
    n = len(a)
    # 정방행렬만 가능
    for row in a:
        assert len(row) == n

    # 2X2 는 직접 가능
    if n == 2:
        return a[0][0]*a[1][1] - a[0][1]*a[1][0]

    result = 0
    for i in range(n):
        sign = (-1) ** i
        coeff = a[0][i]
        # 재귀적으로 계산
        result += sign * coeff * det(submatrix(a, i))
    return result

위처럼 직접 계산할 수 있긴한데, 이 방법은 곱셈이 많아서 소수점 아래로 오차가 많아져서 overflow를 피하기 어렵다.

다른 방법으로는 라이프니츠 공식으로 N X N 크기 행렬의 행렬식을 구할 수 있다.
어떻게 전개되는 지는 아래 유튜브에 잘 설명되어 있다.

Leibniz formula for computing determinants  | Lecture 30 | Matrix Algebra for Engineers

numpy 를 설치하지 못하는 등의 상황이라면, 라이프니츠 공식의 pyhton 구현체도 많이 찾아볼 수 있다.

Finding determinant of a nxn matrix using Leibniz formula on python

# https://github.com/python/cpython/blob/main/Modules/itertoolsmodule.c
def permutations(iterable, r=None):
    pool = tuple(iterable)
    n = len(pool)
    r = n if r is None else r
    if r > n: return
    indices = list(range(n))
    cycles = list(range(n, n-r, -1))
    parity = 0
    yield tuple(pool[i] for i in indices[:r]), parity
    while n:
        for i in reversed(range(r)):
            cycles[i] -= 1
            if cycles[i] == 0:
                if ((n-i) & 1) == 0: parity = 1 - parity
                indices[i:] = indices[i+1:] + indices[i:i+1]
                cycles[i] = n - i
            else:
                j = cycles[i]
                parity, indices[i], indices[-j] = 1 - parity, indices[-j], indices[i]
                yield tuple(pool[i] for i in indices[:r]), parity
                break
        else: return

# 행렬식 계산
def determinant(mat):
    n = len(mat)
    def dosign(parity, x): return -x if parity else x
    det = 0
    for sigma, parity in permutations(range(n)):
        mul = 1
        for i in range(n):
            mul *= mat[i][sigma[i]]
        det += dosign(parity, mul)
    return det

numpy 패키지와 비교하면 오차가 미세하게 있지만, 재귀식으로 구현한 함수보다는 훨씬 낫다.