logit vs. sigmoid vs. softmax

Logit

logit 함수를 이해하려면 odds 를 알아야한다. logit 함수는 \( logit(p) = log(odds) \)  이기 때문이다.

Odds

odds 는 어떤 사건이 발생할 확률과 발생하지 않을 확률을 비교한 값이다. 일반적으로는 성공 확률을 실패 확률로 나누어서 계산한다고 한다.

$$ odds = \frac{p}{1-p} $$

여기에 로그를 씌운 함수를 logit function 이라고 부른다.

$$ logit(p) = log(odds) = log(\frac{p}{1-p}) $$

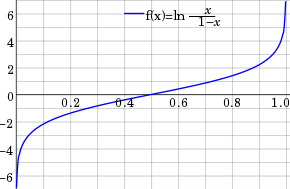
이 logit function 을 x=[0, 1] 에 대해서 그래프를 그려보면 아래와 같이 생겼다.

x=[0, 1] 일 때의 logit(x)

Sigmoid

sigmoid 함수는 logit function의 역함수이다. 즉, x와 y를 뒤집은 그래프라는 것이다.

$$ sigmoid(x) = \frac{1}{1+e^{-x}} $$

역함수임을 보이기 위해 logit function 으로부터 유도해보자면 아래와 같다.
logit function의 결과물(치역)을 \( X \) 로 놓고 역함수를 유도한다.

$$ logit(p) = log(\frac{p}{1-p}) = X $$

식을 전개해보면 다음과 같이 \(X\)에 대한 식을 구할 수 있다.

$$ \begin{align} X &= log(\frac{p}{1-p}) \\ e^{X} &= \frac{p}{1-p} \\ \frac{1}{e^X} &= \frac{1-p}{p} = \frac{1}{p} - 1 \\ \frac{1}{e^X} + 1 &= \frac{1}{p} \\ \frac{1+e^X}{e^X} &= \frac{1}{p} \\ p &= \frac{e^X}{1+e^X} = \frac{1}{1+e^{-X}} \end{align} $$

sigmoid 함수에 대한 설명은 많이 있는데, logit function 의 생김새를 떠올려보면 함수의 결과값이 [0, 1] 사이로 매핑되는 것을 직관적으로 이해할 수 있다.

x=[-6, 6] 일 때의 logistic function

그래프 설명에 Logistic 함수라고 적은 이유는, sigmoid 함수는 logistic 함수의 일부이기 때문이다. 
요약하자면, sigmoid 함수는 logistic 함수에 제약을 건 부분 집합이라고 생각하면 된다.
자세한 설명은 아래의 링크를 참고하면 좋다.

What are the differences between Logistic Function and Sigmoid Function?

그렇다면 당연하게도 \( sigmoid(logit(p(x))) = p(x) \) 라는 뜻이다.

Softmax

분류 문제에서 자주 사용되는 정규화 함수이다.

간단하게 정리하면 sigmoid 함수는 이진 분류(binary classfication)에 사용되고, 분류해야할 클래스가 2개 이상이라면 softmax를 사용한다.

 

출처: https://towardsdatascience.com/sigmoid-and-softmax-functions-in-5-minutes-f516c80ea1f9

위에서 알아본 바와 같이, sigmoid 함수는 어떤 사건이 발생할 확률과 그렇지 않을 확률을 계산한 odds 로부터 확장된 함수이기때문에 이진 분류에 사용된다.

sigmoid 와 동일한 방식으로, 여러 클래스를 벡터로 보고 계산하면 아래와 같이 된다.

출처: https://towardsdatascience.com/sigmoid-and-softmax-functions-in-5-minutes-f516c80ea1f9

사건 발생 확률의 전체 합이 1.0 이 되지 않는다. 왜냐하면 \(X\) 는 logit function을 통과한 값이고, 그렇다면 output은 분명 아래와 같다.

$$ e^X = e^{log(odds)} = odds $$

output vector의 각 element가 odds 그대로인 상황이다.

그래서 사용되는 것이 softmax 함수이고, 다음과 같이 생겼다.

$$ softmax(x) = \frac{ e^{x_i} } { \sum_{j=1}{K} e^{x_j} } $$

이제 softmax 를 통과한 input vector는 전체 확률의 합이 1.0 으로 계산된다.

출처: https://towardsdatascience.com/sigmoid-and-softmax-functions-in-5-minutes-f516c80ea1f9

Reference

Sigmoid and SoftMax Functions in 5 minutes

Sigmoid function - Wikipedia

 

Logit - Wikipedia

What does Logits in machine learning mean?

Softmax function - Wikipedia