Joonas' Note
BOJ 11012 - Egg 본문
https://www.acmicpc.net/problem/11012
문제
2차원 평면에서 점들의 위치가 주어지고, [left, right]×[bottom, top] 으로 그려지는 사각형 내에 있는 점의 개수를 쿼리마다 출력하는 문제이다.
이 문제는 PST(Persistent Segment Tree)로 해결할 수 있다.
PST의 이해를 위해서는 Segment Tree를 먼저 알아야한다. 이 글에서는 자세한 설명은 생략하고, 도움이 될 만한 글로 대체한다. 사실 같은 내용을 이 문제에 대해서만 다시 정리하는 것이라 봐도 무방하다.
혼동이 있을 수 있지만, 이 글에서는(필자는) 세로/수직 방향을 \(y\)축으로 가로/수평 방향을 \(x\)축으로 한다. 즉, \((0,~0)\)은 왼쪽 아래를 의미한다.
y축을 따라서 각 열마다, 아래부터 \(i\)번째 행까지 등장한 점의 개수를 누적하여 저장하면 아래 그림과 같이 표현할 수 있다.

빨간색 사각형 안의 점의 개수는, \(y=4\) 위치의 \(x=[1,~3]\) 구간의 합에서 \(y=2\) 위치의 \(x=[1,~3]\) 구간의 합을 뺀 것과 같다.
이건 누적 합으로 부분 합을 구하는 것을 생각하면 이해가 빠를 것이다.
문제는 구간 합(주황색 영역과 노란색 영역)을 어떻게 구하느냐인데, 각 행(y축)마다 세그먼트 트리를 구성한다면 가능할 것이다.
그럼 전체 노드의 개수는, 리프 노드가 가로 \(W\)개인 세그먼트 트리가 높이 \(H\)개 있으므로 \(2N^2\)가 필요해서 메모리에 무리가 있어보인다.
이를 PST로 해결할 수 있다.
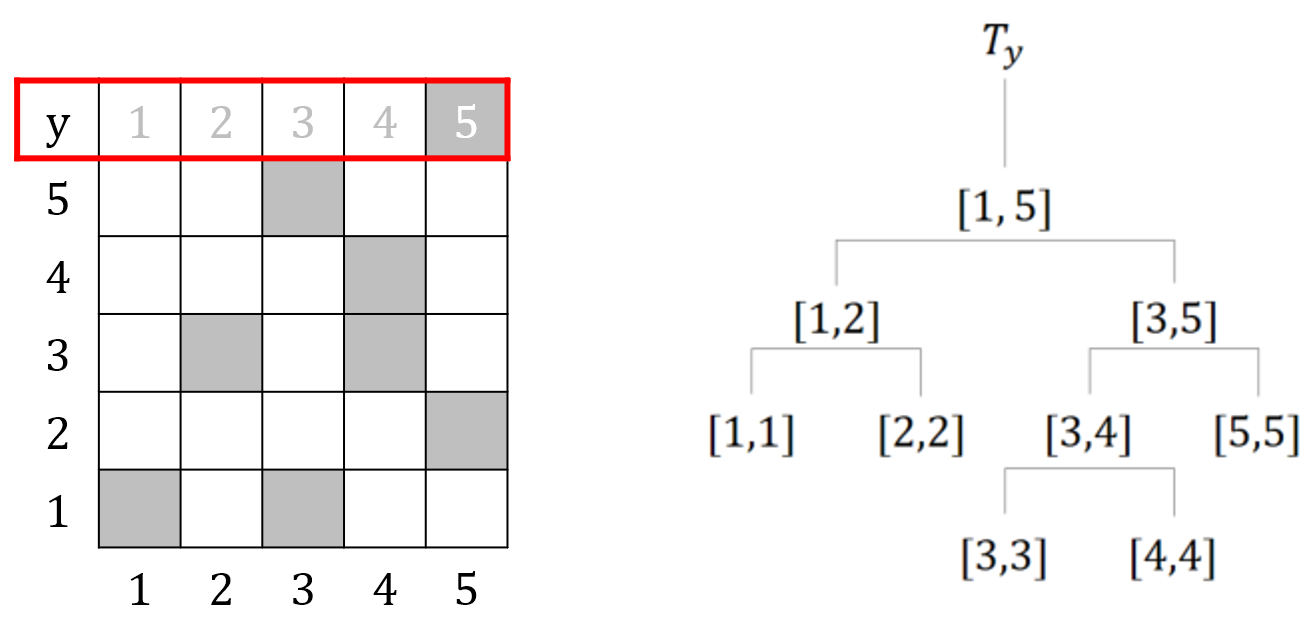
어떤 \(y\)축에 대한 세그먼트 트리를 \(T_y\)라고 부르면, 위 그림처럼 그려질 것이다.
트리에서 \([a, b]\)는 해당 노드가 표현(저장)하고 있는 구간을 의미한다.
이전 트리의 상태를 활용하는 PST의 특징을 이용하면, 메모리도 줄이면서 누적 합처럼 저장할 수 있다.

2차원 좌표에 점이 아래와 같이 있는 상황에서 예시를 확인해보자.

초기 상태인 \(T_0\)은 모든 값이 0이다.
\(T_{y=1}\)부터 \(T_5\)까지 차례대로 트리를 만들어본다면, 아래와 같다. 여기서 트리 중간에 나오는 \(T_y\)는, 이전 \(T_y\) 트리의 그 위치로 이어진다는 뜻이다.
트리가 새로 만들어지면서 생긴 노드들은 빨간색으로 표현하였다. 노드가 저장하는 값은 노드가 표현하고 있는 범위에 있는 점들의 개수이다.

이렇게 트리를 구축한다면, 매번 새로 생기는 \(lgN\)개의 노드가 세그먼트 트리의 수만큼 있으므로, \(NlgN\)의 공간만 사용할 수 있다.
이렇게 만든 PST를 사용해 특정 영역에 있는 점의 개수를 구해보자.
[left, right]×[bottom, top]이 [2, 4]×[2, 4]인 경우에는, 아래처럼 구할 수 있다.

\(T_4\)에서 \(x=[2, 4]\) 구간의 합은 1+3=4 이다. \(T_1\)에서 \(x=[2, 4]\) 구간의 합은 1 이다.
따라서 빨간색 사각형 내에는 4-1=3개의 점이 있다고 구할 수 있다.
다른 예시도 확인해보자.
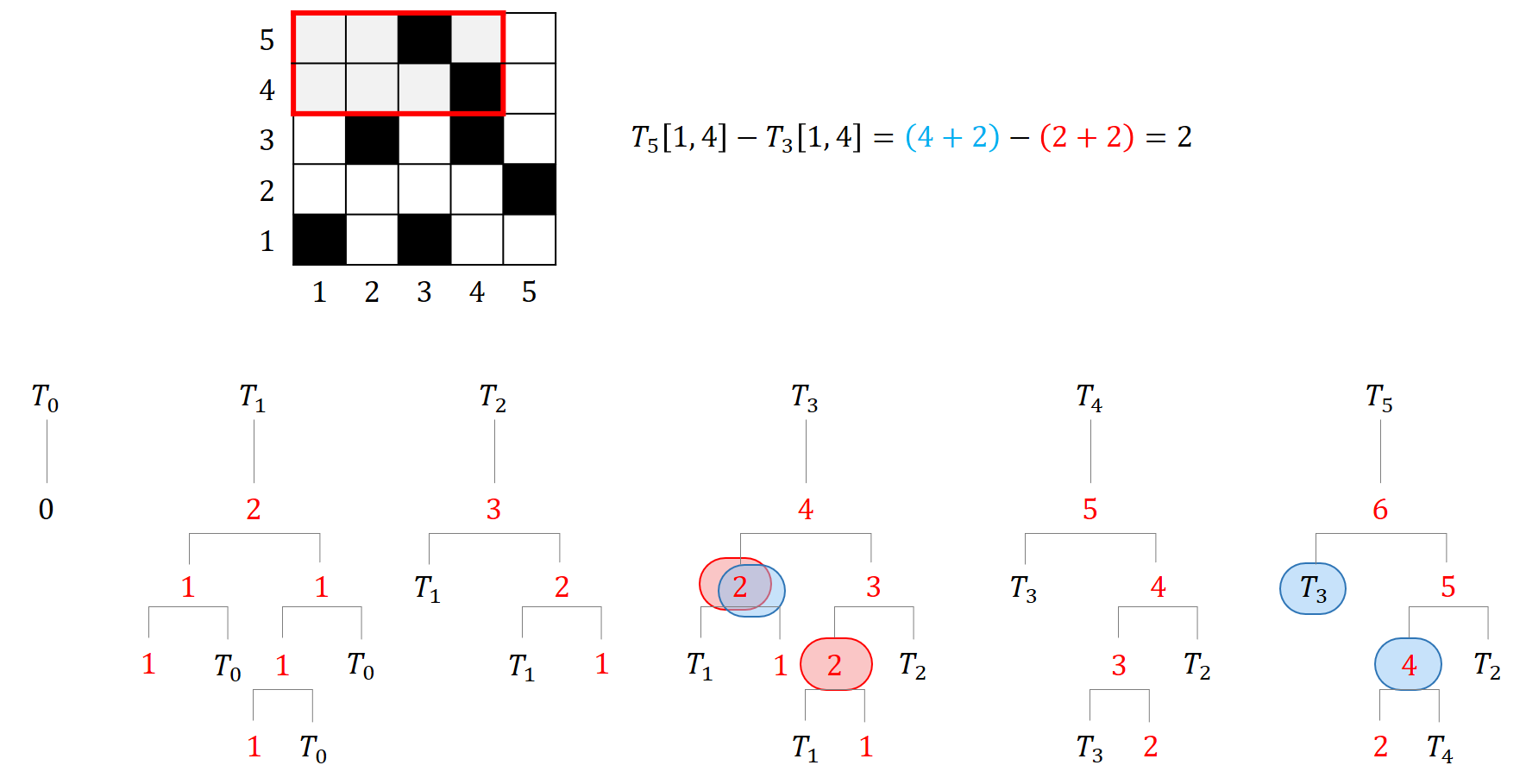
6-4=2개로 잘 나오는 것을 확인할 수 있다.
이 문제에서 조심할 점은, 좌표가 겹칠 수 있다.
새로운 노드를 만들 때, 이전 노드의 값 + 1을 제대로 하지 못해서 계속 틀렸다.
x와 y의 좌표가 0인 점도 있을 수 있으므로, \(T_0\)을 적절히 잘 처리하는 것도 글과 조금 다르니 조심해야한다.
코드
'알고리즘 > 문제 풀이' 카테고리의 다른 글
| BOJ 2133 - 타일 채우기 (0) | 2021.09.07 |
|---|---|
| UVa 136 - Ugly Numbers (2) | 2020.07.06 |
| [코딩으로 풀어보기] 95화 4번, 1~9까지 숫자로 식을 성립시켜라. (0) | 2020.06.10 |
| BOJ 3640 - 제독 (0) | 2020.05.24 |
| BOJ 15480 - LCA와 쿼리 (0) | 2020.05.15 |



