Joonas' Note
BOJ 2133 - 타일 채우기 본문
링크: https://www.acmicpc.net/problem/2133
문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구하는 문제이다.
풀이
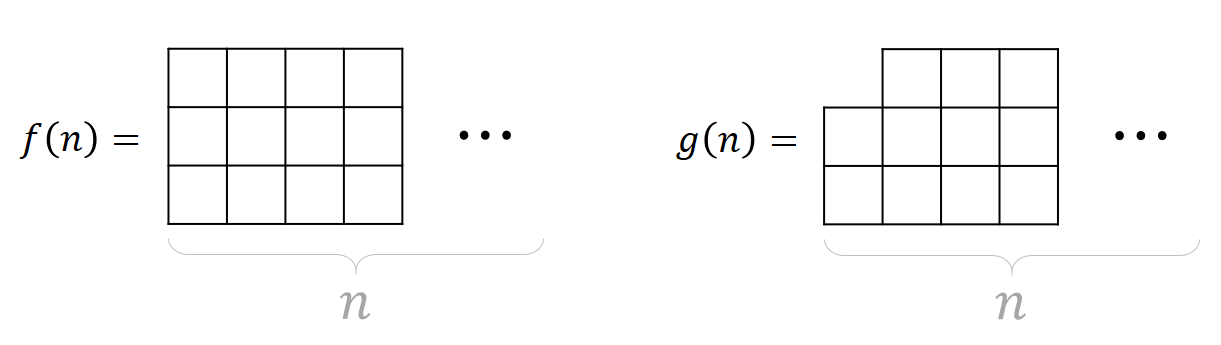
3×N 벽을 채우는 경우를 \(f(n)\), 한 칸이 빈 3×N 벽을 채우는 경우를 \(g(n)\) 라고 하자.
왼쪽부터 2×1 또는 1×2 크기의 타일을 하나씩 채워보면서 가능한 경우를 살펴본다.


\(g(0)\)와 \(g(2)\)는 타일을 채울 방법이 없으므로 \(g(0) = g(2) = 0\) 이다.
이것을 식으로 나타내면 이렇다.
$$f(n) = \begin{cases} 0 & \text{if $n$ < 2} \\ 2g(n-1) + f(n-2) \end{cases}$$
$$g(n) = \begin{cases} 1 & \text{if $n$ = 1} \\ 0 & \text{if $n$ < 3} \\ g(n-2) + f(n-1) \end{cases}$$
이대로 코드를 구현해서 \(f(n)\)을 구하면 정답이다.
풀이 2
두 함수가 상호 참조하는(꼬여있는) 형태가 아니라 하나의 점화식으로 합칠 수 있다.
\(N\)이 홀수일 때는 답이 항상 나올 수 없으므로, 짝수에 대해서 점화식을 하나로 합쳐보자.
먼저 \(g(n)\)에 대해서 점화식을 한 쪽으로 정리한다.
여기서 \(n\)은 \(f(n)\)에서 \(g(n-1)\)을 계산하므로 \(g(n)\)을 전개할 때는 홀수로 가정해야한다.
$$\begin{align} g(n) & = g(n-2) + f(n-1) \\ & = g(n-2) + \{ 2g(n-2) + f(n-3) \} \\ &= g(n-2) + 2 \cdot (g(n-2) + g(n-4) + g(n-6) + \cdots + g(1) ) + f(0) \\ &= g(n-2) + 2 \cdot (g(n-2) + g(n-4) + g(n-6) + \cdots + 1 ) + 0 \end{align}$$
\(f(0) = 0\) 이라서 식에 \(g(n)\) 꼴만 남는다. \(g(n)\)과 \(g(n-2)\)를 전개해서 둘을 상쇄시킬 것이다.
$$\begin{align} g(n) & = g(n-2) + 2 \cdot (g(n-2) + g(n-4) + \cdots + g(1)) \\ g(n-2) & = g(n-4) + 2 \cdot (g(n-4) + g(n-6) + \cdots + g(1)) \end{align}$$
이제 \(g(n) - g(n-2)\)를 구해보면 식이 정리된다.
$$\begin{align} g(n) - g(n-2) & = g(n-2) - g(n-4) + 2 \cdot g(n-2) \\ \therefore ~ g(n) & = 4 \cdot g(n-2) - g(n-4) \end{align}$$
이렇게하면 \(g(n)\)에 대한 점화식을 구할 수 있다.
그런데 여기서 굳이 \(f(n)\)을 다시 계산할 필요가 없다.
왜냐하면, \(g(n)\)은 한 칸이 없는 3×N 크기의 벽을 채우는 것인데,
여기서 그냥 2칸이 더 없다고 생각하면 (또는 타일 하나를 그냥 미리 두었다고 생각하면), \(f(n-1)\)과 같은 모양이기 때문이다.

즉, \(g(n+1)\) 만 구해서 출력하면 그것이 정답이 된다.
코드
코드에서 g[n]의 값은 여태 설명한 그림(한 칸이 없는 3×N 크기의 벽)과는 다르다.
결과적으로 \(f(n)\)을 저장하기 때문에, 초기 값으로 \(g(3) = 3\) 이 들어간다.
참고로 이 문제로 만들어지는 수열은 OEIS A001835 수열과 같다.
다른 문제
- BOJ 2133번 - 타일 채우기 (3×N 크기의 벽) [풀이]
- BOJ 2718번 - 타일 채우기 (4×N 크기의 벽) [풀이]
- BOJ 13976번 - 타일 채우기 2 (3×N 크기의 벽) [풀이]
- BOJ 14852번 - 타일 채우기 3 (2×N 크기의 벽) [풀이]
- BOJ 15700번 - 타일 채우기 4 (N×M 크기의 벽)
'알고리즘 > 문제 풀이' 카테고리의 다른 글
| BOJ 13976 - 타일 채우기 2 (0) | 2021.09.07 |
|---|---|
| UVa 136 - Ugly Numbers (2) | 2020.07.06 |
| BOJ 11012 - Egg (1) | 2020.06.10 |
| [코딩으로 풀어보기] 95화 4번, 1~9까지 숫자로 식을 성립시켜라. (0) | 2020.06.10 |
| BOJ 3640 - 제독 (0) | 2020.05.24 |



